Capita sovente, nelle operazioni di adeguamento sismico, di incappare in pareti (portanti) realizzate con mattoni pieni e spessore di 12 cm, le quali si presentano in buone condizioni statiche e, per vari motivi dovuti ad esigenze di carattere architettonico od a vincoli imposti dalle ditte confinanti, non possono essere demolite.
Questi setti sono presenti sia a sostegno di solai di legno, sia come pareti “di taglio” e, pur essendo costituite da elementi di laterizio aventi resistenza a compressione molto elevata, non possono essere impiegate nel loro stato in essere a causa della loro snellezza (h/t), che risulta di solito molto elevata, con valori intorno a 15÷20, specie nel caso di sostituzione dei solai esistenti con quelli di latero-cemento.
Non potendo purtroppo sostituire tali pareti con una struttura di laterizio del tipo “a monoblocco”, occorre dunque trovare il sistema di consolidarle, cercando di agire il più possibile nel rispetto dei principi fondamentali degli interventi antisismici su edifici esistenti.
La prima cosa da evitare (ma spesso proposta in cantiere!) è di affiancarvi un setto di calcestruzzo armato: non si ritiene necessario entrare in complicati approfondimenti ma basti ricordare a quale scompenso torsionale (chi riesce a indovinare veramente la posizione del centro di massa?) sarebbe soggetta una fragile struttura muraria come quella tipica dei vecchi fabbricati sui quali bisogna intervenire.
Semmai sarebbe più corretto realizzare un betoncino (di gran lunga il sistema migliore quando la muratura ha spessore sufficiente!) ma probabilmente non si risolverebbe il problema della snellezza (la parete diventerebbe spessa circa 3+12+3 = 18 cm). Inoltre, molto spesso la realizzazione del betoncino è osteggiata per vari motivi, non ultimo, ad esempio, quello della difficoltà dell’alloggiamento dell’impianto elettrico.
Una soluzione frequentemente impiegata è, invece, quella che prevede di consolidare la muratura utilizzando una parete di laterizio semipieno da ammorsare in parallelo a quella esistente. In questo modo si evita anzitutto di provocare sensibili scompensi nella distribuzione delle rigidezze dei setti murari. Per i seguenti motivi:
- il peso proprio dei blocchi POROTON® semipieni è ridotto ma le caratteristiche di resistenza a compressione sono sempre molto elevate, non troppo dissimili da quelle dei mattoni pieni (vds. Tab. 1 della Circ. Min. n. 21745 del 30/7/1981). Se si ragiona con l’ottica del D.M. 20/11/1987 si ha che, da caratteristiche simili di resistenza caratteristica a compressione, si ottengono moduli elastici simili (E = 1000•fk). Se invece si ragiona in base ai dettami del D.M. 2/7/1981 la differenza tra i moduli risulta più accentuata poiché si parte dalla resistenza caratteristica al taglio (E = 6•G, G = 1100•fvko). In ogni caso occorre far presente che il rapporto tra Emmax/Emmin risulterà pari a circa 1.67 mentre il rapporto tra il modulo E del calcestruzzo e quello della muratura a mattoni pieni risulta almeno pari a 9 (Rck = 250 daN/cm² e muratura con fk = 30 daN/cm²);
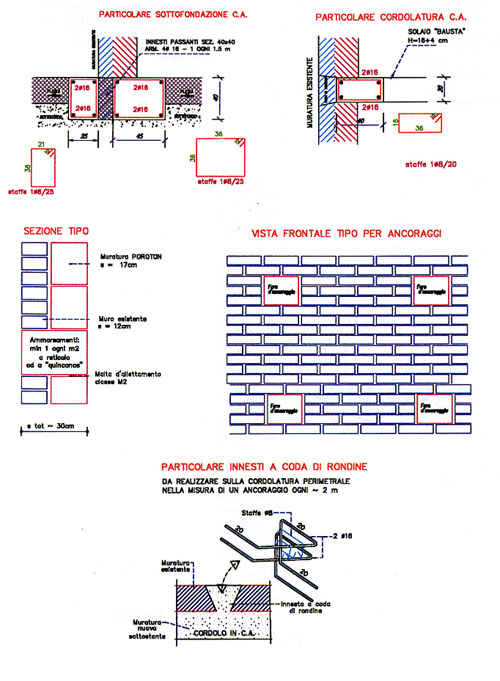
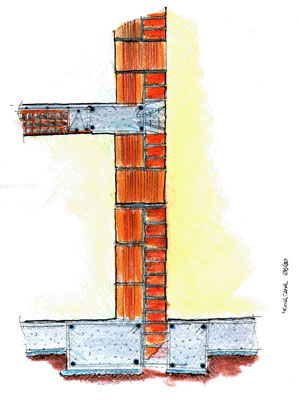
- quando si realizzano la fondazione ed il cordolo, tutta la parte nuova di muratura viene rispettivamente a gravare sulla prima e a poggiare sul secondo. Gli ancoraggi a coda di rondine completano poi le operazioni di ammorsamento.
Per contro abbiamo una maggiore onerosità dell’intervento, se questo è paragonato alla demolizione e ricostruzione con nuova muratura del tipo a monoblocco che, però, non sempre si può realizzare.
È chiaro che molta attenzione deve essere posta nelle operazioni di ammorsamento tra le due parti murarie: quella esistente e quella nuova in parallelo.
A tale scopo (si vedano anche i disegni esplicativi – figura 1) occorrerà che gli ancoraggi siano almeno nella misura di uno ogni metro quadrato, con sistema a reticolo o a “quinconce”. Connettere le due parti murarie è importante soprattutto per quanto riguarda l’instabilità Euleriana al carico di punta. Si può supporre che, realizzando gli ancoraggi come previsto, la lunghezza libera di inflessione di una parete si riduca dall’altezza di interpiano (di solito variabile tra i 2,2 ed i 2,5 metri) ad 1 metro al massimo.
Con ciò si può pensare di aver in ogni caso, rispettivamente, ridotto snellezza ed aumentato il carico critico, come traspare dal seguente esempio comparativo. Indichiamo, infatti, con indice “A” una parete di mattoni pieni da 12 cm con H = 250 cm, e con “B” un’analoga parete ma con H = 100 cm.
- Confronto tra i carichi critici: Pcrit(B)/Pcrit(A) = [π²•E•J/(β•HB)²]/[π²•E•J/(β•HA)²] = (HA/HB)² ≅ 6.25
- Confronto tra le snellezze: HA/t = 250/12 = 20.8 >> 12; HB/t = 100/12 = 8.33
L’esempio appena fatto ha solo valore comparativo in quanto è evidente che non si può ragionare in termini di carico critico Euleriano per una parete muraria. In questo caso, infatti, si raggiungerebbe un carico limite che porterebbe ad una tensione di compressione notevolmente superiore a quella ammissibile dal sistema costruttivo.
Cioè si avrebbe (nel caso più sollecitato, con H = 250 cm):
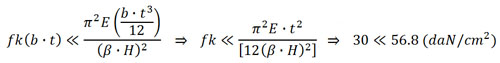
In ogni caso la drastica riduzione della lunghezza libera d’inflessione ha sicuramente un effetto benefico sulla stabilità del sistema composto parete mattoni pieni–semipieni. Ciò significa che, se da un lato gli ammorsamenti non ci restituiscono una parete omogenea come quella con spessore a “monoblocco”, d’altro canto si viene a creare comunque un sistema resistente e sufficientemente stabile alle azioni verticali: senz’altro molto più performante rispetto al semplice accostamento di due pareti (è impressionante talvolta vedere quale situazione statica reale si trovino a fronteggiare queste pareti di mattoni pieni da 12 cm!…).
Per quanto attiene alla resistenza al taglio delle connessioni, si nota che un ancoraggio presenta un’area resistente pari ad A = b•h = 340 cm² (in questo caso: b = 17 cm, h = 20 cm).
Supponendo una crisi da taglio con un valore fvko = 2.0 daN/cm², si ha a disposizione una resistenza ultima V pari a: V = A•fvko = 680 daN.
Ipotizzando di avere almeno due ancoraggi sulla verticale per una fascia unitaria (1 m), si ottiene che la resistenza a disposizione corrisponde (anzi, è superiore!) alla reazione d’appoggio di un generico solaio di l.c. per abitazione (G+Q = 650 daN/m²) con una luce di 4 metri: R = 1.0•650•(4.0/2) = 1300 daN
In ogni caso meglio non invocare l’instaurarsi di cedimenti differenziali ed assicurarsi che le opere di sottofondazione risultino idonee a garantire un adeguato coefficiente di sicurezza.






