
Per il calcolatore delle strutture che deve affrontare il problema di operare un intervento strutturale antisismico, sia che si tratti di “miglioramento” che di “adeguamento”, su edifici risalenti al periodo intercorrente tra gli anni ’50 ed i primi anni ’70, e che si imbatte in murature realizzate con blocchi tipo “bimattone” a fori orizzontali (foratoni) il problema che si pone è quello di “quantificare” il grado di resistenza dei muri realizzati con siffatti elementi.
L’unico appiglio viene dato, ancora una volta, dalla famosa “Tabella 1” della Circ. Min. n. 21745 del 30/07/1981 dalla quale trarre prudenzialmente, come limite superiore, i valori τk = 8 t/m² (0,8 daN/cm²) e σk = 250 t/m² (25 daN/cm²), che risultano i più “bassi” per murature in laterizio.
È bene ricordare che, almeno in alcune regioni italiane (nel caso specifico in Veneto), questo tipo di blocco è stato utilizzato massicciamente per la realizzazione di piccoli o medi edifici fino a tre piani di altezza.
Volendo approfondire la questione, e non avendo trovato risposte esaurienti nella letteratura consultata in materia, si è avuta l’occasione per poter eseguire alcune prove di compressione su questo tipo di elementi, anche grazie alla disponibilità del collega Ing. Bruno De Paris2 che ha fornito un muretto per la prova ed al Laboratorio “R’bk” di Limana (BL) che ha messo a disposizione le proprie specifiche e moderne attrezzature, coordinandone l’esecuzione [fig. 1].


a) vista esterna;
b) le attrezzature.
I materiali e le prove sui blocchi
In occasione di un intervento di ristrutturazione sono stati recuperati otto blocchi. Di questi, sette sono stati rettificati con successo mentre l’ultimo risultava già danneggiato così da non poterlo sottoporre alla prova.
I blocchi non erano mai stati usati e si trovavano accantonati in una soffitta ben asciutta ed in ottimo stato di conservazione. Da notizie raccolte dal proprietario dell’edificio, tali blocchi potrebbero grosso modo risalire come datazione alla fine anni ’50 – primi anni ’60.
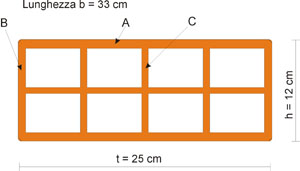
Le caratteristiche di tali blocchi [fig. 2], rilevate dopo l’opportuna rettifica, sono riassunte in tab. 1.
| Blocco B1 | Blocco B2 | Blocco B3 | Blocco B4 | Blocco B5 | Blocco B6 | Blocco B7 | |
|---|---|---|---|---|---|---|---|
| Dim. | 25×11,4×33,8 | 25,4×11,6×33,4 | 25×11,4×32,8 | 25,5×11,8×33,3 | 24,8×11,5×33 | 25×11,5×33 | 25,4×11,5×33 |
| A | 8 mm | 10 mm | 8 mm | 8 mm | 8 mm | 9 mm | 8 mm |
| B | 11 mm | 10 mm | 11 mm | 11 mm | 10 mm | 11 mm | 11 mm |
| C | 7 mm | 9 mm | 7 mm | 8 mm | 7 mm | 7 mm | 7 mm |
Legenda:
Dim: dimensioni (spessore t x altezza h x lunghezza b)
A: spessore medio pareti esterne orizzontali
B: spessore medio pareti esterne verticali
C: spessore medio setti interni

I risultati delle prove a compressione sui 7 campioni esaminati sono riassunte in tab. 2.
| Blocco | t (cm) | b (cm) | A = t x b (cm²) | N (daN) | fb = N/A (daN/cm²) |
|---|---|---|---|---|---|
| B1 | 25,0 | 32,8 | 820,0 | 48000 | 58,5 |
| B2 | 25,4 | 33,4 | 848,4 | 58000 | 68,4 |
| B3 | 25,0 | 32,8 | 820,0 | 32500 | 39,6 |
| B4 (*) | 25,5 | 33,3 | 849,2 | 35300 | 41,6 |
| B5 (*) | 24,8 | 33,0 | 818,4 | 33700 | 41,2 |
| B6 (*) | 25,0 | 33,0 | 825,0 | 30300 | 36,7 |
| B7 (*) | 25,4 | 33,0 | 838,2 | 28300 | 33,8 |
(*) Risultati ottenuti con la seconda pressa.
Le prove sono state eseguite con un gradiente di carico unitario pari a 200 kPa/s = 2,0 daN/cm², come previsto dalle norme. Dal blocco B4 é stato necessario utilizzare una seconda macchina di prova in quanto nella prima si erano danneggiati degli elementi ammortizzanti.
Dai risultati delle prove si ricava un valore della resistenza media a compressione dei blocchi pari a:
In questo caso, essendo il numero dei provini considerati minore di 30, non ha significato utilizzare la formula per la valutazione della resistenza caratteristica a compressione fbk del blocco:
dove:
con s = scarto quadratico medio (cfr. D.M. 20/11/1987, Allegato 1, punto 1.2.1)



Volendo comunque “azzardare” una stima della resistenza caratteristica a compressione di una muratura costituita da tali blocchi e da una malta di tipo M2 (cementizia) od M3 (bastarda), prendendo come riferimento, a livello puramente teorico, la Tabella A del D.M. 20/11/1987, ed ipotizzando come valore plausibile una resistenza caratteristica a compressione del blocco pari a:
si ritiene di poter stimare per la muratura in questione un valore di resistenza caratteristica a compressione fk non superiore a:
cui corrisponderebbe una tensione ammissibile della muratura non superiore a:
La prova su muretto
Come accennato, grazie alla collaborazione di un collega (l’ing. Bruno De Paris), è stato possibile reperire, dai lavori di ristrutturazione di un edificio residenziale risalente agli anni ’60, un muretto costituito dallo stesso tipo di blocchi (foratoni) precedentemente sottoposti a prova di compressione; i blocchi costituenti il muretto risultavano avere la stessa geometria e tipologia dimensionale ed erano caratterizzati da nervature (cartelle e setti) leggermente più consistenti rispetto ai singoli campioni di blocco precedentemente esaminati (mediamente le cartelle perimetrali dei blocchi sono risultate di spessore pari a 12 mm, quelle interne di spessore 10 mm).
Il muretto era costituito da un parallelepipedo di altezza pari a 4 corsi, profondo 2 corsi, e dotato di malta di spianamento sia inferiormente che superiormente. Lo spessore strutturale del muro era di 25 cm (al netto dell’intonaco). Le dimensioni, BxTxH, erano pari a 68,5x25x58 cm (spessore di 29 cm in presenza di intonaco).
Da un esame ispettivo il muretto si presentava in buone condizioni anche se dotato di allettamenti di malta piuttosto consistenti (anche 2/3 cm), poco regolari (con inclinazione del blocco) e la malta stessa aveva un aspetto ed una consistenza poco cementizia.
La prova è stata eseguita con un gradiente di deformazione pari a 0.5 mm/minuto. Il provino è stato avvolto con un telo di plastica avente l’unico scopo di evitare la dispersione di frammenti del campione al momento del raggiungimento della rottura. La superficie del piatto di prova presentava un’area pari a:
Durante l’esecuzione della prova il muretto ha raggiunto un valore di carico a rottura N pari a circa:
da cui risulta una tensione media di rottura:
ed una tensione ammissibile stimabile non superiore a:
Tale valore è sostanzialmente in linea con le attese e con i valori stimabili in base alla resistenza a compressione rilevata sui singoli blocchi.


L’analisi FEM in campo elastico lineare di un blocco tipo a fori orizzontali

Per verificare l’attendibilità dei dati sperimentali acquisiti ed accertare anche la possibilità di svolgere, in mancanza di altri dati, stime teoriche dotate di una certa attendibilità, si è proceduto a svolgere una analisi agli elementi finiti (FEM) in campo elastico lineare applicata ad un blocco tipo a fori orizzontali del tutto analogo a quelli sottoposti a prova [fig. 9].
Le condizioni assunte per l’esecuzione dell’analisi sono di seguito sintetizzate.
- Codice Impiegato: CIVILSOFT 6.0 con solutore Algor Supersap; analisi lineare conservativa in campo elastico; vincoli di appoggio rigidi; 407 nodi, 440 elementi. La linearità del calcolo eseguito consente di interpolare i risultati tensionali moltiplicandoli per il rapporto (N/Ncalc), dove N è il nuovo eventuale carico mentre Ncalc = 10000 daN, è il carico di progetto.
- Dimensioni elemento in esame: 25x33x12 cm; spessore cartelle esterne 11 mm, spessore cartelle interne 7 mm.
- Condizione di carico: peso proprio elemento + N = 10000 daN uniformemente ripartito sui 99 nodi di superficie superiore.
- Controllo di qualità: assicurato. Deformate simmetriche e secondo le aspettative; nessuna incongruenza o squilibrio nodale e nessun errore di calcolo durante l’esecuzione.
Considerando che il carico di rottura medio tra quelli ottenuti dalle prove è pari a:
ed impiegando quale carico totale di riferimento nel modello il valore Ncalc = 10000 daN, per la linearità del metodo di calcolo adottato, per confrontare i valori di tensione e/o di deformazione riscontrati sperimentalmente con quelli ottenuti nel calcolo FEM, questi ultimi dovranno essere moltiplicati per il rapporto tra carico reale applicato e quello di calcolo pari a:
Calibrazione del modello
In base ai dati sperimentali derivanti dalle prove a rottura svolte sui blocchi è stato possibile ricavare un valore del modulo elastico E del materiale che si ritiene abbastanza aderente alla realtà.
La calibrazione non influenza in modo significativo l’analisi tensionale ma serve nella fattispecie ad ottenere un andamento delle deformazioni più veritiero.
Considerando i grafici carico/deformazione rilevati nelle prove sui blocchi B1 e B2 [fig. 10], si nota che, trascurando il primo tratto orizzontale legato all’assestamento della pressa, l’andamento è di tipo lineare con rottura fragile molto decisa, il che consente di confermare la correttezza dell’ipotesi di controllo mediante un’analisi agli elementi finiti in campo elastico lineare.
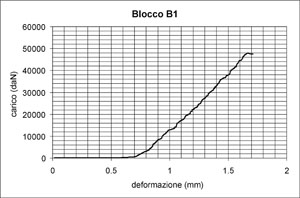
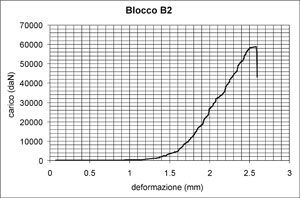
a) prova su blocco B1;
b) prova su blocco B2.
Tenendo conto che lo spostamento massimo tra inizio e fine prova è pari a circa:
si ottiene:
e, per la legge di Hooke (σ = Eε), con riferimento al blocco B1 (carico N = 48000 daN ed area della sezione delle cartelle verticali Ac = 141,90 cm²), si ha:
da cui:
L’andamento “teorico” delle deformazioni ricavato dall’analisi ad elementi finiti [fig. 11] fornisce un valore medio di abbassamento per la faccia superiore del blocco pari a:
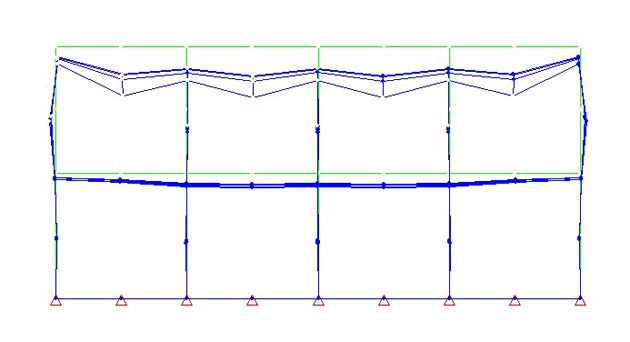
Tenendo conto del rapporto K tra carico sperimentale medio e carico utilizzato nel calcolo teorico, si ottiene il valore di abbassamento medio corrispondente al blocco sottoposto al carico Nmed (valore medio tra le prove effettuate), che risulta:
pressochè coincidente con quello effettivamente misurato in laboratorio.
Considerazioni sulle tensioni di compressione
Le prove sperimentali hanno fornito i seguenti risultati in termini di tensioni:
- tensione di compressione per area lorda (Alorda = 25 x 33 = 825 cm²):
σlorda = Nmed / Alorda = 46,08 daN/cm² - tensione di compressione per area netta (solo area della sezione delle cartelle verticali):
Anetta = 33 x [2 x (1,1) + 3 x (0,7)] = 141,90 cm²
σnetta = Nmed / Anetta = 267,89 daN/cm²
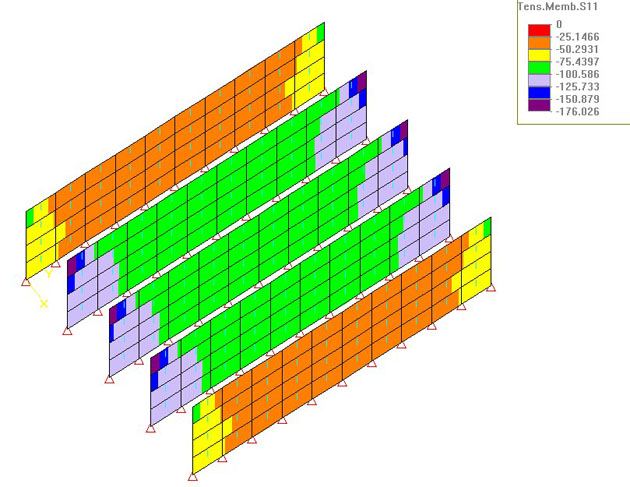
Si analizzano ora i risultati puntuali ricavati dall’analisi FEM; nella fattispecie si considerano le tensioni (principali) vettorializzate secondo la direzione verticale Z, esaminando solo le cartelle verticali [fig. 12].
Tenendo sempre conto del coefficiente di rapporto K = 3,80 precedentemente definito, si ha:
- valore medio di tensione per le cartelle esterne (s = 1,1 mm):
σ’max(e)» K x 37,7 = 143,3 daN/cm² - valore medio di tensione per le cartelle interne (s = 0,7 mm):
σ’max(i)» K x 88,0 = 334,4 daN/cm²
Il valore medio generale ponderato risulta (Ae, sezione cartelle esterne = 72,60 cm², Ai, sezione cartelle interne = 69,3 cm²):
Lo scostamento tra valore “teorico” e valore desunto dalle prove sperimentali è dunque dell’ordine dell’11%; si tratta inoltre di una differenza “a favore della sicurezza”, risultando il dato teorico inferiore a quello sperimentale.
Conclusioni
Per quanto attiene alle prove sui singoli blocchi, i risultati ottenuti sono stati al di sopra delle aspettative, anche se, ovviamente, la resistenza meccanica è modesta e la rottura finale è stata sempre marcatamente di tipo fragile, in particolare per i primi due blocchi che sono letteralmente “scoppiati”.
A prescindere dal numero di blocchi provati, in generale, occorre porre attenzione al singolo blocco caso per caso. Molte volte, come confermava anche l’Arch. Clai del “Laboratorio R’bk”, l’aspetto stesso del blocco non é indicativo del risultato finale: talvolta mattoni con un aspetto mediocre a prima vista danno poi ottimi risultati alla fine della prova. E viceversa. Molto può dipendere dalla composizione chimica delle argille, dalla loro provenienza, dal processo produttivo e nella fattispecie dalle fasi di cottura e raffreddamento.
Non è quindi possibile ed agevole fare una correlazione tra i dati di una prova come questa e la “popolazione” in generale delle murature che sicuramente è soggetta ad una dispersione statistica considerevole.
Anche la geometria dei fori poi ha un’importanza notevole: nel caso in questione una lieve inclinazione delle cartelle verticali può dare luogo sotto sforzo ad importanti effetti del secondo ordine ed invalidare la “bontà” del materiale base.
Ma, come già rimarcato precedentemente, per fare un muro non bastano i mattoni: occorre anche un buon legante e che sia correttamente impiegato.
Per quanto attiene quindi alla prova sul muretto, è chiaro che non si possono fare considerazioni di ordine statistico su una sola investigazione, ed occorre ricordare come in questo caso il valore di rottura del provino, a parere dello scrivente, possa essere stato fortemente influenzato dalla malta.
Sta di fatto che, ragionando in maniera pratica e da “strutturisti”, si ritiene che comunque per muri di questo tipo, in seno ad operazioni di “miglioramento” od “adeguamento sismico” non sia prudente spingersi oltre la tensione ammissibile di progetto/verifica di 2 ¸ 3 daN/cm².
Volendo infine proiettare i risultati come una norma del buon costruire per le nuove costruzioni in muratura si ritiene opportuno insistere ancora una volta sui seguenti punti:
- avere un buon blocco è condizione necessaria ma non sufficiente per avere un buon muro;
- è preferibile impiegare blocchi “a fori verticali” (per esempio POROTON®);
- occorre utilizzare una buona malta (meglio la M2, che ha prestazioni meccaniche prossime a quelle dei blocchi, riduce il ponte termico ed è ben lavorabile);
- curare sia l’allettamento orizzontale sia quello verticale;
- è necessario che l’allettamento della malta sia il più orizzontale possibile, per conservare i blocchi il più possibile verticali;
- è necessario che lo spessore della malta sia compreso tra 0,5 ed 1,5 cm (preferibilmente 1 cm costante).
L’analisi ad elementi finiti ha infine dimostrato un buon grado di congruenza e di attendibilità nella valutazione del comportamento meccanico e deformativo dei blocchi, e consente quindi di ipotizzarne l’impiego in altri casi in cui le informazioni disponibili risultino carenti o scarsamente affidabili.
Note
- “Laboratorio R’bk” per esperienze e ricerche sui materiali.
Referente per la prova: Arch. Giorgio CLAI
32020 Limana (BL) – Loc. Cesa – Via U. Bracalenti, 36
Tel. 0437 967627 – Fax 0437 960399 – E-mail: info@rbk.it
Lab. in concessione Min. LL.PP. con D.M. 21/7/’77 N. 16595 (Art. 20 L. 1086/’71) - Il muretto della prova è stato gentilmente procurato da:
Studio di Ingegneria Ing. Bruno De Paris
Via Garibaldi, 70 – Belluno (BL)






