La normativa energetica italiana
L’estate 2005 è stata segnata non tanto da torride temperature, quanto piuttosto da roventi discussioni attorno ai due importanti decreti pubblicati in rapida sequenza nei mesi di luglio e agosto, in materia di comportamento termico degli edifici.
La ricerca presentata in questo articolo muove da una considerazione generale riguardo la coerenza dei due diversi sistemi di valutazione della prestazione energetica dell’edificio dal momento che il DM 27 luglio 2005, attuativo dell’art. 4 Legge 10/1991, adotta come metodo di calcolo e valutazione, il coefficiente di dispersione termica Cd in netto disaccordo non solo con il DLgs 192/2005 (di seguito DLgs 192) ma con la direttiva europea e il panorama certificativi internazionale che da tempo ha sostituito il coefficiente Cd con un sistema di certificazione basato sulla richiesta energetica misurata in kWh/m2 anno.

Disaccordo che, di fatto, ha provocato una situazione di stallo operativo, dal momento che la mancata emanazione dei decreti attuativi di cui all’art. 4 comma 1 del D. Lgs 192 per la definizione dei criteri generali, della metodologia di calcolo e dei requisiti minimi finalizzati al contenimento dei consumi di energia e la predisposizione di Linee Guida Nazionali per la certificazione energetica degli edifici (art. 6 comma 9) ha mantenuto di fatto valide le norme transitorie previste al Titolo II art. 11.
Indi per cui, in attesa della emanazione dei suddetti decreti, restano valide le prescrizioni del DM 27 luglio 2005 (G.U. 2 agosto 2005) modificate come dall’All. C. D. Lgs 192.
Le disposizioni di cui all’art. 11 punto 5 dell’all. I consentono in realtà di bypassare la procedura di calcolo del fabbisogno annuo di energia primaria.
In attesa che vengano specificati i metodi e le formule di calcolo per la valutazione del fabbisogno annuo di energia, infatti, è possibile adottare il metodo di calcolo semplificato in regime stazionario (UNI EN 832), per verificare che il solo valore della trasmittanza termica U(1) a ponte termico corretto(2) delle strutture delimitanti il volume riscaldato verso l’esterno, ovvero verso ambienti non dotati di impianto di riscaldamento, sia inferiore o uguale a quello riportato nelle tabelle 2, 3 e 4 dell’All. C in funzione della fascia climatica di riferimento.
| Zona climatica | Dal 1° gennaio 2006 U (W/m2K) | Dal 1° gennaio 2009 U (W/m2K) |
|---|---|---|
| A | 0,85 | 0,72 |
| B | 0,64 | 0,54 |
| C | 0,57 | 0,46 |
| D | 0,50 | 0,40 |
| E | 0,46 | 0,37 |
| F | 0,44 | 0,35 |
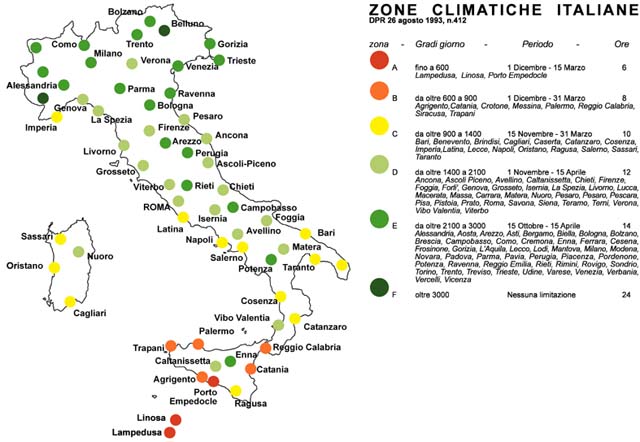
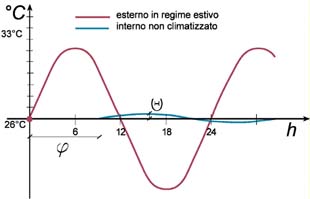
Questo per quanto concerne il regime invernale, ma l’elemento di assoluta novità introdotto dal D. Lgs 192 sta nel recepimento dell’art. 18 della Direttiva 2002/91/CE relativo al rendimento termico degli edifici in periodo estivo.(3) Per la climatizzazione estiva, infatti, il punto 11b dell’All. I prevede che “per tutte le categorie di edifici [.] al fine di limitare i fabbisogni energetici per la climatizzazione estiva e di contenere la temperatura interna degli ambienti, si procede a verificare che: nelle zone climatiche A, B, C, D, nelle località dove il valore medio mensile dell’irradianza sul piano orizzontale Ims, nel mese di massima insolazione, sia maggiore o uguale a 250 W/m2, la massa superficiale Ms(4) delle pareti opache verticali, orizzontali e inclinate, [.] sia superiore a 230 kg/m2.”(5)
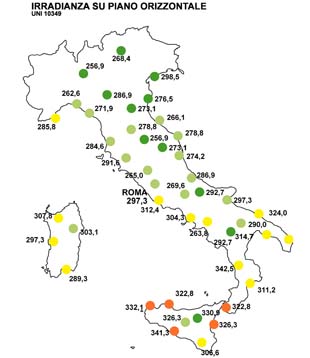
L’aver introdotto anche il comportamento estivo come criterio discriminante per la verifica energetica (anche se tutt’ora assente l’indicazione sulla metodologia da adottare – metodo ASHRAE, metodo di Fanger e altri) pone l’accento sulla impossibilità di trasferire direttamente in climi mediterranei le tecnologie e i materiali delle costruzioni ad alto isolamento e sottolinea la necessità di ripensare il concetto di “casa passiva” studiando nuove (o antiche) soluzioni costruttive che trovino nella massa la caratteristica discriminante.
Osservando poi i dati riportati in fig. 3 appare evidente come “non necessariamente le città a latitudine maggiore (irradianza minore) corrispondano a zone climatiche più fredde. Questa considerazione è di notevole importanza perché evidenzia come il metodo utilizzato da questa norma, ossia la scelta di basarsi sulla latitudine e quindi sull’irradianza come principale parametro di valutazione dei carichi termici ambientali e non sulla zona climatica e quindi sui gradi giorno, differisce dall’approccio della normativa per il calcolo dei consumi energetici in regime invernale”,(7) tanto da includere nella fascia a irradianza superiore addirittura città quali Trento e Milano.
Le procedure di calcolo
In questa linea, nell’ambito della ricerca ANDIL sul ciclo di vita dei prodotti in laterizio(8), è stata condotta una valutazione comparativa, con soluzioni a contorno univoche [vedi tab. 2], sulle prestazioni in regime invernale di trasmittanza termica e di flusso termico uscente per unità di superficie e sulle caratteristiche in regime estivo, di attenuazione e sfasamento dell’onda termica (espresso in termini di smorzamento e ritardo di fase) e di flusso termico entrante relativamente a sei soluzioni tecniche di pareti di tamponamento in laterizio.
| Esposizione | Superficie | Altezza ambiente | Zona termica | T°MG in gennaio UNI 10349 | T°MM estiva UNI 10349 |
|---|---|---|---|---|---|
| sud | 1 m2 | 2,70 m | Firenze (D) | 5,3°C | 33,6°C |
Le simulazioni sono state condotte in regime statico, verificando il comportamento di 1 m2 di parete, nell’ottica di una valutazione delle prestazioni del componente volta ad una qualificazione indicativa del rendimento globale dell’edificio, a meno del fattore correttivo dovuto alla presenza dei ponti termici.
Per il calcolo della massa superficiale Ms [kg/m2] e della trasmittanza U [W/m2K] è stato impiegato il software WinPar, integrando la banca dati esistente con valori di conducibilità λ, densità δ, e calore specifico c direttamente ricavati dal mercato.
Per il calcolo del flusso termico in regime invernale è stata utilizzata la formula:
assumendo
La formula esprime il flusso termico dovuto al passaggio del calore attraverso una generica superficie opaca, ove:
i è la generica parete disperdente
Ui è la trasmittanza della generica parete disperdente [W/m2K]
Si è la superficie della generica parete disperdente, misurata all’interno del locale (uguale a 1 m2)
chi è un fattore che tiene conto dell’altezza del locale considerato (trascurabile)(10)
cei è un fattore che tiene conto dell’esposizione della parete considerata (per pareti esposte a sud cei = 1)
ta è la temperatura ambiente di progetto [°C]
te è la temperatura esterna [°C]
Per le verifiche del comportamento estivo delle pareti sono state impiegate le formule Wright per il calcolo dello smorzamento:
con:
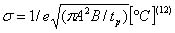
e la formula di Mackey
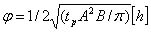
per il calcolo del ritardo di fase o sfasamento.
Smorzamento e sfasamento, valutati combinatamente, in relazione ai parametri λ, c e δ dei materiali che compongono la parete, indicano la capacità di un elemento di abbattere la temperatura del flusso di calore entrante dall’esterno e ritardarne temporalmente il passaggio all’interno in modo che la consegna d’energia verso l’interno avvenga soltanto durante le ore fresche notturne [fig. 4].
In linea generale, una parete presenta smorzamento e sfasamento dell’onda termica tanto più accentuato quanto più piccola è la sua diffusività termica α [m2s] definita dalla relazione:
Ne consegue che una parete costituita da materiale di elevata capacità termica (c x δ [J/kg m3]) attenuerà il propagarsi delle onde termiche esterne fungendo da volano termico, contrariamente invece ad una parete a bassa capacità termica che non potrà svolgere una altrettanto efficace azione smorzatrice.
Dal momento che la norma, ad oggi, non fornisce indicazioni specifiche in merito al comportamento degli edifici in regime estivo od ai parametri che debbano essere verificati per assicurare il comfort interno, e utilizza come unica discriminante la massa superficiale, per il calcolo del flusso termico estivo è stata impiegata la formula di Fourier, che parametrizza il Δt di calcolo in base, appunto, alla massa dell’elemento secondo il “Metodo della Differenza di Temperatura Equivalente”.
La formula:
con:
S superficie disperdente (uguale a 1 m2)
U trasmittanza della parete [W/m2K]
Δteq differenza di temperatura equivalente [°C]
inserisce infatti un valore Δteq che esprime la differenza di temperatura che dovrebbe esistere tra interno ed esterno, nelle condizioni precisate, per avere, attraverso la parete del tipo considerato, lo stesso flusso termico che si ottiene nella realtà e che porta in conto l’apporto solare variabile ciclicamente durante la giornata, l’escursione termica giornaliera dell’aria esterna e le caratteristiche inerziali delle strutture di delimitazione del volume interno riferite al peso per m2 di superficie.
Questo metodo, derivante dal “Cooling Load Temperature Difference Method (CLTD)” dell’ASHRAE, muove dalla considerazione che, nella pratica costruttiva, i vari tipi di pareti perimetrali utilizzati possono essere riuniti, in funzione dei loro principali parametri geometrici e termofisici, in “gruppi” che presentano caratteristiche simili tra loro. Per ciascuno di tali gruppi, attraverso la formula di Fourier, è possibile valutare il flusso termico entrante in regime stazionario ricavando il valore di Δteq da tabelle reperibili sull’ASHRAE Handbook.
I casi studio
Le caratteristiche (materiche, geometriche, dimensionali, prestazionali) degli elementi che compongono ciascuna soluzione, sono riportate nelle figg. 5, 6, 7, 8, 9 e 10.
La scelta dei materiali e dei relativi spessori è stata orientata al soddisfacimento dei requisiti prestazionali minimi espressi dalla tab. 2 dell’All. C al D. Lgs 192.
Ad esclusione della sola soluzione 1, tutte le pareti sono state realizzate con blocchi a fori verticali alleggeriti in pasta, di diverso spessore (dai cm 14 nella soluzione 2 ai cm 30 nelle soluzioni 3 e 6, ai cm 38 della soluzione 5 fino ai cm 45 della soluzione 4), rettificati (soluzioni 2 e 4), sagomati maschio femmina (soluzioni 3 e 6) o ad incastro (soluzione 5), murati a malta semplice (soluzioni 2, 5 e 6) o a malta termica (soluzioni 3 e 4).
Per il raggiungimento dei valori prescritti di U, le soluzioni 3 e 4 hanno richiesto, inoltre, la realizzazione di uno strato esterno di intonaco termoisolante di cm 3 e 2 rispettivamente.
La soluzione 6 è stata realizzata impiegando blocchi con le cavità riempite di schiuma isolante di produzione tedesca ma disponibili sul mercato italiano.
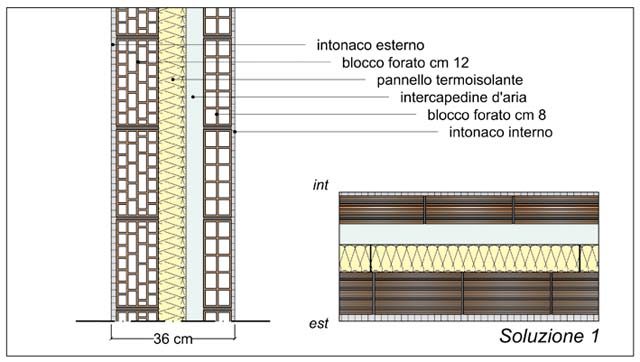
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce | 0,010 | 0,700 |
| 2 | Blocchi forati in laterizio | 0,080 | 0,360 |
| 3 | Intercapedine d’aria | 0,050 | 0,270 |
| 4 | Isolamento termico | 0,080 | 0,052 |
| 5 | Blocchi forati in laterizio | 0,120 | 0,360 |
| 6 EST | Intonaco calce e cemento | 0,020 | 0,700 |
Zona climatica D
| Spessore s | 0,360 | m |
| Massa superficiale Ms | 180,7 | kg/m² |
| Resistenza termica R | 2,322 | m²K/W |
| Trasmittanza U | 0,400 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
5,880 | W |
| Smorzamento Θ = θ0 x σ | 4,409 | °C |
Ritardo di fase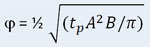 |
2,081 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 6,080 | W |
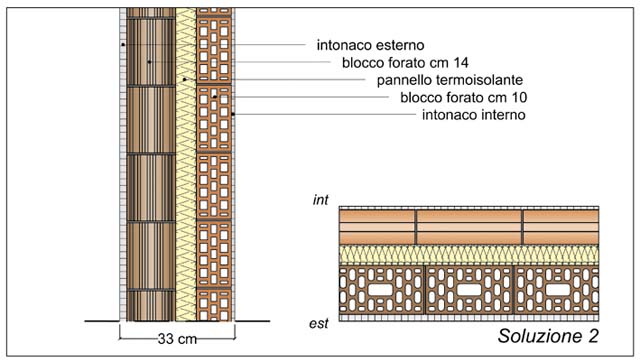
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce | 0,010 | 0,700 |
| 2 | Blocchi alleggeriti | 0,100 | 0,390 |
| 3 | Isolamento termico | 0,060 | 0,037 |
| 4 | Blocchi alleggeriti | 0,140 | 0,360 |
| 5 EST | Intonaco calce e cemento | 0,020 | 0,700 |
Zona climatica D
| Spessore s | 0,330 | m |
| Massa superficiale Ms | 245,6 | kg/m² |
| Resistenza termica R | 2,310 | m²K/W |
| Trasmittanza U | 0,400 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
5,880 | W |
| Smorzamento Θ = θ0 x σ | 1,116 | °C |
Ritardo di fase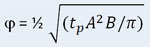 |
7,331 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 6,080 | W |
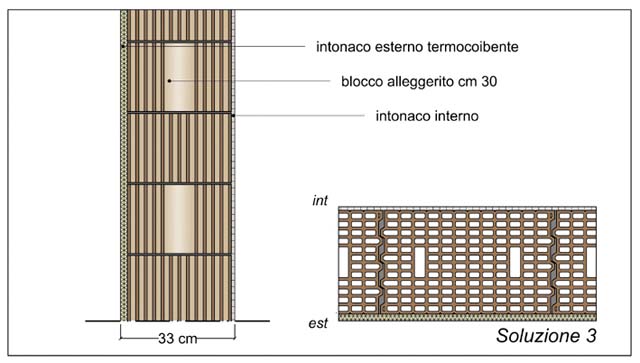
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce | 0,010 | 0,700 |
| 2 | Blocchi alleggeriti murati con malta termica | 0,300 | 0,220 |
| 3 EST | Intonaco termoisolante | 0,030 | 0,066 |
Zona climatica D
| Spessore s | 0,340 | m |
| Massa superficiale Ms | 279,5 | kg/m² |
| Resistenza termica R | 1,832 | m²K/W |
| Trasmittanza U | 0,500 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
7,350 | W |
| Smorzamento Θ = θ0 x σ | 0,180 | °C |
Ritardo di fase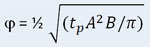 |
14,309 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 7,600 | W |
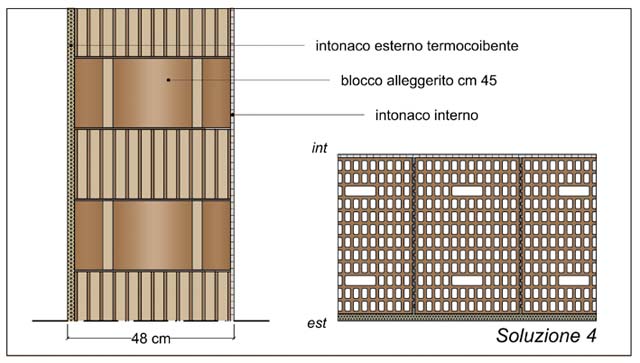
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce | 0,010 | 0,700 |
| 2 | Blocchi alleggeriti murati con malta termica | 0,450 | 0,220 |
| 3 EST | Intonaco termoisolante | 0,020 | 0,066 |
Zona climatica D
| Spessore s | 0,480 | m |
| Massa superficiale Ms | 401,7 | kg/m² |
| Resistenza termica R | 2,088 | m²K/W |
| Trasmittanza U | 0,395 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
5,807 | W |
| Smorzamento Θ = θ0 x σ | 0,074 | °C |
Ritardo di fase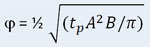 |
17,718 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 3,792 | W |
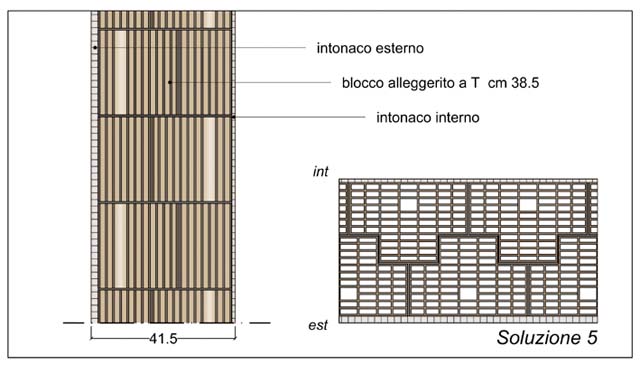
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce | 0,010 | 0,700 |
| 2 | Blocco alleggerito ad incastro | 0,380 | 0,185 |
| 3 EST | Intonaco calce e cemento | 0,020 | 0,900 |
Zona climatica D
| Spessore s | 0,410 | m |
| Massa superficiale Ms | 354,0 | kg/m² |
| Resistenza termica R | 2,091 | m²K/W |
| Trasmittanza U | 0,443 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
6,512 | W |
| Smorzamento Θ = θ0 x σ | 0,494 | °C |
Ritardo di fase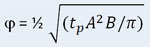 |
10,448 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 4,253 | W |
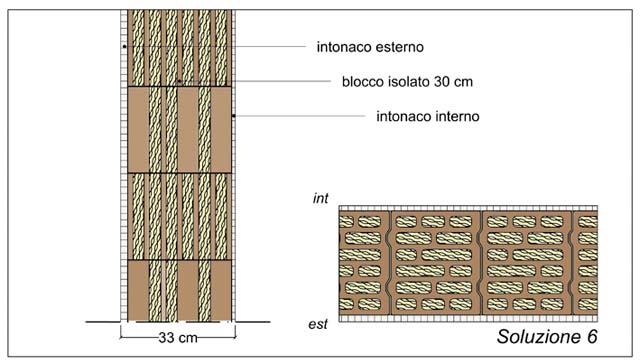
| Ordine degli strati | Materiale | Spessore (m) | λ (W/mK) |
|---|---|---|---|
| 1 INT | Intonaco calce e gesso | 0,010 | 0,700 |
| 2 | Blocchi alleggeriti termoisolanti | 0,300 | 0,107 |
| 3 EST | Intonaco calce e cemento | 0,020 | 0,700 |
Zona climatica D
| Spessore s | 0,330 | m |
| Massa superficiale Ms | 282,0 | kg/m² |
| Resistenza termica R | 2,847 | m²K/W |
| Trasmittanza U | 0,332 | W/m2K |
| Flusso termico in regime INVERNALE Qd = cei x Ui x Si x (ta-te) |
4,880 | W |
| Smorzamento Θ = θ0 x σ | 2,116 | °C |
Ritardo di fase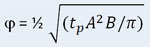 |
4,887 | h |
| Flusso termico in regime ESTIVO Q(θ) = U Δteq (θ) | 5,046 | W |
Considerazioni finali
Emerge dallo studio una volontà normativa di privilegiare, almeno in climi mediterranei, il ricorso di soluzioni costruttive “massive” anche se il decreto, tralasciando le indicazioni correttive riportate dal DM 27 luglio 2005 (art. 4, Tab. 2) per il calcolo del valore U in relazione alla massa frontale dell’elemento, consente di fatto un controllo solo parziale della riduzione dei consumi per il raffrescamento degli edifici.
Il metodo di calcolo semplificato per la verifica in regime stazionario, infatti produce risultati [tab. 3] che possono essere solo indicativi del reale comportamento della parete in opera e dell’edificio nel suo complesso, dal momento che, trascurando la capacità termica e riportando le prestazioni dell’elemento alle sole correzioni previste dalle tabelle ASHRAE sulla base delle categorie di peso per m2 (100-300-500-700 kg/m2), non fornisce indicazioni su quello che realmente accade all’interno dell’ambiente. Risultano infatti, in termini di legge, parimenti ammissibili soluzioni quali la n. 6, con un flusso in estate (5,046 W) superiore a quello invernale (4,880 W), a fronte di soluzioni come la n. 4 o la n. 5 che consentono invece una riduzione della potenza termica in estate del 34% circa rispetto a quella invernale e mentre queste ultime presentano, assieme alla soluzione n. 3, valori ottimali anche dal punto di vista dello sfasamento dell’onda termica, con un ritardo che si attesta intono alle 12 ore considerate ideali, la soluzione n. 6, cedendo densità in favore di una minore conducibilità, sconta, conseguentemente, uno smorzamento poco efficace (2,116°C) e un ritardo di fase poco soddisfacenti in termini di comfort interno (4,887 h).
Analogamente, le soluzioni “leggere” (soluzioni 1 e 2), ottimali dal punto di vista dell’isolamento termico in virtù di considerevoli spessori di materiale isolante interposto, possono soffrire in regime estivo di una massa superficiale che i buoni valori di trasmittanza (0,400 W/m2K) non riescono a compensare nel calcolo stazionario in termini di flusso entrante (in entrambi i casi si registra un incremento di potenza del flusso estivo) ma che, in relazione a scelte oculate dei singoli materiali (orientate ad alte densità), a parità di trasmittanza, possono comunque produrre incrementi prestazionali significativi di sfasamento e smorzamento (46,3% e 74,6% rispettivamente della soluzione n. 2 rispetto alla n. 1).
In conclusione, le formule riportate nel presente studio costituiscono senza dubbio un metodo efficace e veloce di calcolo in fase progettuale, per una verifica preliminare delle prestazioni dei componenti che orienti alla scelta dei materiali in relazione ai vincoli e alle limitazioni sia normative che volumetriche che condizionano il progetto, ferma restando la necessità, per una verifica globale del comportamento dell’edificio, di un calcolo in regime dinamico che tenga conto non solo dei risultati prestazionali dei singoli componenti, ma delle relazioni che i componenti stessi stabiliscono tra loro dal punto di vista strutturale e geometrico e delle influenze che queste relazioni comportano in termini di dispersioni, accumuli e bilanci termici.
| Ms kg/m2 |
U W/m2K |
Qi W |
Qe W |
φ h |
|
|---|---|---|---|---|---|
| Soluzione 1 | 180,70 | 0,400 | 5,880 | 6,080 | 2,081 |
| Soluzione 2 | 237,80 | 0,396 | 5,821 | 6,019 | 5,369 |
| Soluzione 3 | 279,50 | 0,500 | 7,350 | 7,600 | 14,309 |
| Soluzione 4 | 401,70 | 0,395 | 5,807 | 3,792 | 17,718 |
| Soluzione 5 | 354,00 | 0,443 | 6,512 | 4,253 | 10,448 |
| Soluzione 6 | 282,00 | 0,332 | 4,880 | 5,046 | 4,887 |
Note
- Verificato che il rendimento medio stagionale dell’impianto termico sia non inferiore al valore riportato al punto 5 dell’All. C.
- Qualora il ponte termico non dovesse risultare corretto o qualora la progettazione dell’involucro edilizio non preveda la correzione dei ponti termici, i valori limite della trasmittanza termica riportati nelle tabelle 2, 3, 4 All. C, devono essere rispettati dalla trasmittanza termica media.
- DIRETTIVA 2002/91/CE DEL PARLAMENTO EUROPEO E DEL CONSIGLIO del 16 dicembre 2002 sul rendimento energetico nell’edilizia, art. 18: “Negli ultimi anni si osserva una crescente proliferazione degli impianti di condizionamento dell’aria nei paesi del sud dell’Europa. Ciò pone gravi problemi di carico massimo, che comportano un aumento del costo dell’energia elettrica e uno squilibrio del bilancio energetico di tali paesi. Dovrebbe essere accordata priorità alle strategie che contribuiscono a migliorare il rendimento termico degli edifici nel periodo estivo. Concretamente, occorrerebbe sviluppare maggiormente le tecniche di raffreddamento passivo, soprattutto quelle che contribuiscono a migliorare le condizioni climatiche interne e il microclima intorno agli edifici”.
- Massa per unità di superficie della parete opaca compresa la malta dei giunti ed esclusi gli intonaci espressa in kg/m2.
- Il decreto, inserendo il fattore di massa come elemento caratterizzante il comportamento in regime estivo, recupera una disposizione già presente nel DM 27/07/05 (art. 4 comma 2) che introduceva il coefficiente moltiplicatore Cm per la correzione dei valori della trasmittanza U delle strutture orizzontali e verticali opache in funzione della massa totale della struttura per unità di area (massa frontale).
- I valori dell’Irradianza riportati nella figura sono stati ricavati attraverso la formula Im = 11,57 ΣnH/Σn dai dati tabulati della UNI 10439, con n = numero di giorni del mese preso in considerazione e H = irradiazione solare globale giornaliera media mensile.
- G. Borroni, UNI 10375: come calcolare la temperatura interna estiva, in Tetto & Pareti – tecnologie e prodotti sostenibili per l’involucro casa, dic. 2004.
- LCA laterizio post produzione, Dip. TAeD Università degli Studi di Firenze. Responsabile della Ricerca Prof. Maria Chiara Torricelli.
- Differenza tra la temperatura di progetto 20°C e la temperatura media giornaliera invernale dell’aria esterna (5,3°C in gennaio), UNI 10349.
- Per 3>h>4 m, chi = 0,06 (ta-te)°C/m. Per pareti di altezza inferiore non si tiene conto del gradiente termico (UNI 7357).
- Differenza tra ta = 26°C e la temperatura massima media stagionale estiva dell’aria esterna (33,6°C in luglio), UNI 10349.
- A = ΣR sommatoria delle resistenze termiche dei singoli strati che compongono la parete;
B = 1,1/A x (Si δi ci + S1 δ1 c1 + S2 δ2 c2 + . + Sn δn cn) + (λe δe ce)/A x [Se/λe – 0,1 (Si/λi – 0,1 (S1/λ1) – 0,1 (Sn/λn)];
tp = periodo di oscillazione di temperatura pari a 24 h.






