La muratura è il più antico e diffuso materiale da costruzione. Nel passato il suo impiego ha consentito la realizzazione di opere in cui la valenza architettonica si associava a quella strutturale.
Dopo un lungo periodo nel quale si è ritenuto, a torto, che la muratura avesse esaurito la sua funzione portante, da alcuni anni, si sta riscoprendo il suo carattere strutturale. La rinnovata fiducia nella muratura è la conseguenza di tecnologie costruttive innovative, della possibilità di disporre di materiali con più elevate risorse meccaniche ottenuti con nuove produzioni, di una crescente attenzione degli studiosi alle problematiche degli edifici in muratura, in particolare se soggetti alle azioni sismiche, di un quadro normativo nazionale ed europeo ormai rinnovato od in via di completamento1, 2.
La riscoperta della muratura è anche la conseguenza della perdita della centralità del cemento armato come materiale da costruzione nell’edilizia considerato di elevata durabilità. Le molte manifestazioni di degrado del cemento armato, sempre più frequenti nelle strutture in c.a. di edifici post-bellici, hanno effettivamente spinto i progettisti verso una rinnovata maggiore attenzione nei confronti della muratura come materiale caratterizzato da diverse possibilità di impiego.
La muratura in effetti può essere adottata per i suoi vantaggi nell’isolamento termico, o impiegata negli elementi di partizione degli spazi o anche con funzione portante. È evidente che la muratura come materiale strutturale non presenta le risorse di resistenza e duttilità del cemento armato o dell’acciaio. Ciò nonostante, l’organismo di un edificio in muratura, realizzato attraverso l’unione di elementi bidimensionali, si presenta come un complesso scatolare che permette di confidare su elevati livelli di sicurezza, sia nei confronti delle azioni permanenti verticali che di quelle sismiche. Pertanto, anche se la muratura presenta una bassa resistenza a taglio e flessione, nel suo insieme, è in grado di far fronte alle azioni sismiche, sviluppando un certo grado di duttilità dovuto, in particolare, ai collegamenti fra i pannelli murari.
Attualmente, i materiali di nuova produzione impiegati nella muratura (blocchi e/o malte) permettono di ottenere caratteristiche di resistenza nominali più elevate rispetto al passato. È quindi utile analizzare, sia sperimentalmente che attraverso simulazioni teoriche, il comportamento dei pannelli murari realizzati con i nuovi prodotti presenti sul mercato.

In tale ambito si colloca lo studio che si presenta. In questa sede si analizza, infatti, il comportamento evolutivo non lineare di pareti murarie con presenza di bucature, realizzate con blocchi di laterizio semipieni alleggeriti in pasta, sottoposte ad azioni combinate di compressione e taglio.
L’analisi con codice automatico di calcolo è di tipo non lineare perché in tal modo si ottiene una simulazione completa del comportamento reale attraverso la visualizzazione del processo fessurativo a vari livelli di carico orizzontale.
Pannelli in muratura sottoposti ad azioni di taglio e modello di riferimento
In anni recenti, sulla base di numerose ricerche sperimentali, la muratura, come materiale da costruzione, è stata ampiamente rivalutata: utilizzando, infatti, malte ad alta resistenza e buona qualità di blocchi si possono ottenere resistenze tanto elevate da poterne suggerire l’utilizzo anche per edifici multipiano.
L’eventuale presenza di armatura riesce poi a conferire, in presenza di scuotimento sismico, oltre ad una buona resistenza a flessione e taglio, anche duttilità e capacità di dissipazione di energia3, 4, 5.
Le azioni orizzontali sismiche, sia che risultino applicate direttamente alle pareti e dirette normalmente alle stesse, come conseguenza delle forze sismiche dovute alle masse murarie, o che nascano in corrispondenza degli impalcati, in conseguenza dei carichi permanenti ed accidentali che vi agiscono, vanno affidate alla struttura nel suo complesso con funzionamento scatolare, sempre che gli impalcati siano in grado di svolgere il ruolo di efficaci diaframmi orizzontali e quindi di ripartire le azioni sismiche fra le pareti verticali.
Il comportamento sismico degli edifici in muratura è direttamente legato alla risposta resistente dei singoli pannelli murari sottoposti all’azione di taglio nel proprio piano6÷10.
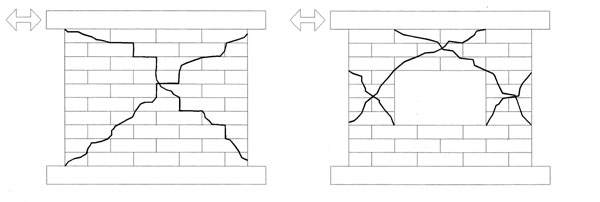
Nelle pareti in muratura prive di aperture, il collasso per taglio, dovuto ad un’azione sismica, si verifica spesso con le modalità indicate in fig. 2a, mentre nei maschi murari e nei setti fra le aperture di una parete il collasso è del tipo mostrato in fig. 2b11.
In generale, possono presentarsi altri meccanismi di rottura di un pannello murario:
- scivolamento per taglio di una porzione di muratura su un letto di malta che avviene, in particolare, quando il carico verticale sul pannello attinge valori bassi e la malta è di scarsa qualità. Questo meccanismo di rottura è comunque raro nei pannelli murari di nuova esecuzione, concepiti con materiali e regole nuove, mentre è purtroppo frequente negli edifici esistenti;
- rottura per flessione che si sviluppa nel caso di alta resistenza a taglio della muratura ed elevato rapporto momento flettente/taglio. In tal caso, si ha fessurazione del pannello sia sul lato teso che compresso. I meccanismi resistenti ed i modi di rottura di pannelli in muratura, in situazione sismica, dipendono da molteplici fattori: la geometria dell’elemento murario, il rapporto altezza spessore, la qualità dei materiali, la presenza di aperture, le condizioni con cui il pannello è vincolato lungo i bordi. Come è noto, si può procedere, per via approssimata, alla valutazione della resistenza delle pareti sottoposte alle azioni sismiche attraverso la definizione del meccanismo resistente effettivo per la struttura. Ad esempio, se l’edificio presenta impalcati rigidi, si può ipotizzare che i maschi murari (murature comprese fra le file verticali di aperture) funzionino come ritti di un telaio a traversi infinitamente rigidi ed in essi si localizzino le fessurazioni conseguenti al meccanismo di rottura per taglio12.
Nei casi reali sono stati rilevati però frequentemente comportamenti prossimi a quello di mancanza di diaframmi rigidi perché, con l’incrementarsi delle azioni sismiche, le fasce di piano, cimentate in misura crescente sino alla loro rottura per flessione e taglio, perdono la loro efficacia di collegamento, consentendo così ai maschi murari un funzionamento prevalentemente flessionale.
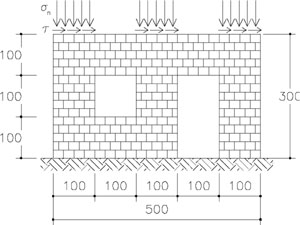
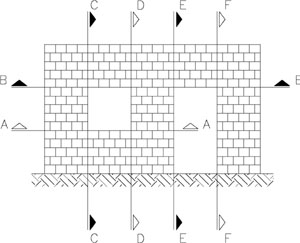
Nell’analisi che si presenta, si è cercato di valutare l’effettivo comportamento sotto carichi orizzontali di pannelli murari costituiti da blocchi alveolari organizzati secondo la tipologia di parete muraria con aperture indicata in fig. 3 e presente nella Circolare LL.PP. 30.07.81, n. 21745.
Nella tab. 1 sono riportati i valori più significativi che qualificano le caratteristiche meccaniche dei blocchi in laterizio alleggerito considerati.
| Foratura dei blocchi | % | < 45 | |
| Impiego | Murature portanti in zona sismica | ||
| Massa volumica apparente dei blocchi | kg/m3 | 800 | |
| Classificazione dei blocchi secondo le norme UNI 8942 | – | BSA 11-31 | |
| Resistenza meccanica dei blocchi | Resistenza a compressione nella direzione dei carichi verticali (fbk) | kg/cm2 | 120 |
| Resistenza a compressione nella direzione ortogonale a quella dei carichi verticali e nel piano della muratura (f’bk) | kg/cm2 | 20 | |
| Coefficiente di variazione δ | – | < 0,20 | |
| Resistenza meccanica della muratura | Resistenza caratteristica (fk) | kg/cm2 | 55 |
| Resistenza caratteristica a taglio in assenza di carichi verticali (fvk0) | kg/cm2 | 2,5 | |
Per l’analisi del comportamento della parete muraria in blocchi di fig. 3, si è fatto riferimento ad un legame costitutivo relativo a dati sperimentali ed espresso con una legge polinomiale del 2° ordine nella forma seguente4, 5:
σ/σu = a (ε/εu)2 + b (ε/εu) + c
con a = -0,154; b = 1,037; c = 0,014 essendo σu ed εu, rispettivamente, la tensione ultima di compressione ed il coefficiente di deformazione lineare.
Si è constatato sperimentalmente che anche una relazione lineare del tipo σ/σu = (ε/εu) può ritenersi sufficientemente corretta per descrivere il comportamento in compressione di una muratura costituita da blocchi del tipo adottato nell’indagine.
Il modello di parete in muratura analizzato è stato studiato utilizzando il codice di calcolo ANSYS che permette di controllare la non linearità della muratura dovuta, in particolare, alla fessurazione delle zone sottoposte a stati di trazione.
Il procedimento di calcolo adottato prevede la definizione del quadro fessurativo per vari passi di carico evidenziando le linee fessurative sul modello geometrico ad ogni avanzamento di carico modificando la matrice di rigidezza del materiale nel legame costitutivo di tipo incrementale che si adotta per l’analisi numerica:
dσ = K dε
Il processo fessurativo reale è ovviamente molto complesso ma viene sostanzialmente descritto nel calcolo in modo completo introducendo dei coefficienti che tengono conto sia degli effetti di ingranamento fra le superfici murarie a contatto nella zona fessurata che delle risorse residue del materiale nella trasmissione delle tensioni di compressione.
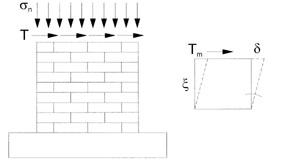
L’analisi della parete organizzata di fig. 3 è stata preceduta dallo studio di un pannello senza aperture, sottoposto ad uno stato di tensione piano con carico verticale costante [fig. 4].
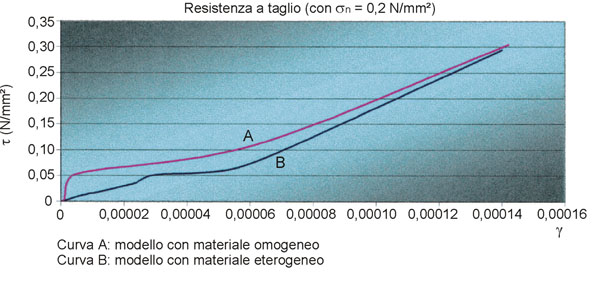
La valutazione del diagramma τ-γ [fig. 5], relativo alla risposta strutturale sotto carico, ha permesso di constatare che l’errore che si commette nel considerare un modello matematico basato su caratteristiche meccaniche medie è del tutto accettabile rispetto ad una modellazione in cui si consideri il pannello anisotropo a causa delle diverse caratteristiche meccaniche della malta e del blocco.
Sulla base dell’ipotesi di materiale omogeneo con caratteristiche meccaniche medie, è stato analizzato il comportamento della parete.
Nell’analisi è stata considerata una pressione verticale s costante sui maschi murari pari a 0,2 N/mm2 ed una forza orizzontale collocata alla sommità della parete, considerata crescente per incrementi successivi di carico pari a 5 kN.
L’analisi condotta ha permesso di valutare il comportamento di una parete organizzata in muratura di laterizi alleggeriti senza formulare alcuna ipotesi preliminare sulla rigidezza delle fasce orizzontali.
Il controllo dell’evoluzione fessurativa è, ovviamente, legato sia alla resistenza della muratura alveolare considerata che alla presenza nella parete muraria di aperture. Infatti, nei casi reali di edifici sottoposti ad azioni sismiche si è più volte constatata l’importanza della presenza e disposizione delle aperture nella risposta strutturale.
Risultati principali, confronti ed osservazioni conclusive
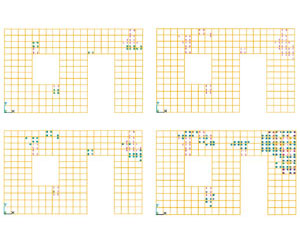
Si riportano alcune visualizzazioni grafiche significative del quadro fessurativo, riferite al modello di parete in muratura in blocchi alveolari di fig. 3.
Nel calcolo si è considerata raggiunta la fessurazione quando localmente la tensione principale di trazione è risultata pari a 0,1 N/mm2. Nelle zone fessurate per trazione, le tensioni tangenziali hanno raggiunto un valore massimo pari a 0,27 N/mm2 ed un valore di tensione a compressione pari a 0,57 N/mm2.
Al fine di confrontare il comportamento di pareti murarie in blocchi di laterizio alleggerito con pareti costituite da diverse tipologie di laterizi, è stata condotta un’ulteriore analisi numerica considerando la parete muraria di riferimento di fig. 3 eseguita con gli elementi resistenti indicati nella tab. 2.
| Tipo | σr (N/mm2) | τr (N/mm2) |
|---|---|---|
| Blocco laterizio alleggerito – A (cm 25 x 30 x 19) (*) | 7,12 | 0,32 |
| Mattone doppio UNI (cm 25 x 12 x 12) | 14,00 | 0,53 |
| Mattone pieno UNI (cm 25 x 12 x 5,5) | 9,70 | 0,38 |
| Blocco laterizio alleggerito – B (cm 25 x 30 x 15) | 6,30 | 0,45 |
| Blocco laterizio alleggerito – C (cm 25 x 30 x 15) | 6,36 | 0,39 |
| Blocco laterizio alleggerito – D (cm 25 x 25 x 12) | 4,80 | 0,17 |
| Blocco quadri UNI (cm 25 x 25 x 12) | 2,40 | 0,44 |
(*) Elemento utilizzato
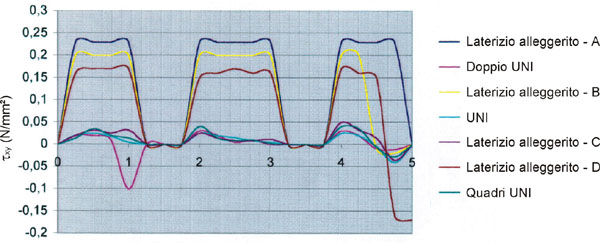
Nella fig. 6 sono indicate le sezioni di riferimento B-B, C-C ed E-E prese in considerazione.
Il confronto fra le varie tipologie di blocchi in laterizio in pareti murarie di identica geometria ha confermato come, in tutti i sistemi, il collasso avvenga per raggiungimento del limite di resistenza a trazione nelle fasce di piano.
La parete costituita da blocchi alveolari si colloca, in termini di risposta tensionale, nella media dei comportamenti.
Il controllo evolutivo sotto carico incrementale di taglio, condotto su modello di parete con bucature in cui non si è formulata alcuna ipotesi restrittiva sulla resistenza della fasce di piano e/o dei maschi murari, consente di affermare che la fessurazione interessa principalmente le fasce di piano in prossimità delle bucature presenti.
La resistenza della parete muraria costituita da blocchi di tipo alveolare alle azioni orizzontali è quindi legata alla resistenza delle fasce orizzontali di parete sollecitate a taglio-flessione mentre ai maschi murari è consentito un comportamento flessionale.
L’analisi effettuata, pur interpretando al meglio l’effettivo comportamento non lineare della muratura, è pur sempre approssimata, poiché si fa riferimento ad un modello semplificato piano che non tiene conto dell’interazione con pannelli trasversali ed i diaframmi di piano. La presenza di solai rigidi ed il collegamento con pareti murarie trasversali, come è noto, influenza la risposta strutturale con riflessi sui meccanismi resistenti dei pannelli alle azioni sismiche.
In conclusione, si può comunque ritenere che per pareti con presenza di aperture, sollecitate a taglio e costituite da blocchi alveolari, il comportamento dei maschi murari è prevalentemente di tipo flessionale e l’integrità strutturale dipende dalla resistenza delle fasce di piano.
Bibliografia:
- European Committee for Standardization, “Eurocode 6. Design of masonry structures, Part 1-1: general rules for buildings – rules for reinforced and unreinforced masonry”, ENV 1996-1-1: 1995 Bruxels: CEN 1995
- European Committee for Standardization, “Eurocode 8. Design provisions for earthquake resistance of structures. Part 1-1: general rules for buildings – seismic actions and general requirements for structures”, ENV 1998-1-1: 1994, Bruxels CEN 1995
- M. Tomazevic, “Seismic design of masonry structures”, Construction Research Communications Limited 1997 ISSN 1365-556, Earthquake Engineering and Structural Dynamics, 88-95, 1977
- B.P. Sinha e R.F. Pedreschi, Deformation and cracking of post-tensioned brickwork beams”, The Structural Engineer, 63, (4), 93-99, 1985
- B.P. Sinha e R.F. Pedreschi, “Predicting the flexural strength of prestressed brickwork beams”, Structural Engineering Review, 4, (3), 211-221, 1992
- V. Turnesek e F. Cacovic, “Some experimental results on the strength of brick masonry walls”, Proc. 2nd Int. Brick Masonry Conference, Stoke on Trent, 149-156,1971
- G. Magenes e G.M. Calvi, “In-plane seismic response of brick masonry walls”, Earthquake Eng. Struc. Dynamics, 26, 1091-112, 1997
- L. Gambarotta e S. Lagomarsino, “Damage models for the seismic response of brick masonry shear walls”, Earthquake Eng. Struc. Dynamics, 26, 423-439, 1997
- G.C. Manos, B. Yasin e J. Thaumpta, “Combined horizontal cyclic and compressive load testing of partially reinforced masonry piers”, Proc. Masonry Society 8th, London, 196-201, 1998
- R. Capozucca e G. Menditto, “Alcune considerazioni sull’analisi della vulnerabilità di strutture in muratura dell’entroterra marchigiano”, L’Ingegneria Sismica, N.2, 41-49, 1998
- M. Wakabayashi, “Progettazione di Strutture Antisismiche”, Mcgraw-Hill, Milano,1989
- M. Tomazevic, “The computer program P.O.R.”, Report ZRMK 1978 (in sloveno)






